c'est sterd qui le dit (et pour une fois je lui donne raison)
c'est la "fameuse" identité d'euler

Alors déja, pourquoi elle est si belle, cette équation ?
Sans doute parce qu'elle réussi a relier de façon simple trois "nombres" remarquables des mathématiques :
le nombre 1 - inutile de le présenter
le nombre pi -c'est pas sorcier non plus, c'est le rapport (constant) entre la circonférence d'un cercle et son rayon
le nombre i
là, c'est plus subtil ! Le nombre i est une construction des mathématiciens qui leur permet de résoudre l'équation i = racine carré de -1
on pose i.i = -1 et le tour est joué !
et on dit que i est un nombre "imaginaire" ! on invente alors l'ensemble des nombres imaginaires, puis les nombres complexes (un nombre complexe est la somme d'un nombre imaginaire plus un nombre réel) c=a+ib -le petit i est la pour rappeler que la partie a droite du + est un nombre imaginaire )
e est "la base des logarithmes néperiens" ou logarithmes "naturels C'est la "primitive" de la fonction 1/x -la valeur de la surface quand X varie de 0 a 1 est égale a ce fameux "e"
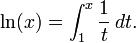
d'ou
ln (1) = e
le premier résultat que euler parvient a établir c'est

d'ou il va parvenir a établir la seconde relation
si vous voulez savoir comment on établi la premiere relation, on en déduit la seconde (ou n'importe quoi d'autre) suffit de le demander a sterd (pour une explication rigoureuse) ou a moi (pour une explication moins rigoureuse)
c'est la "fameuse" identité d'euler

Alors déja, pourquoi elle est si belle, cette équation ?
Sans doute parce qu'elle réussi a relier de façon simple trois "nombres" remarquables des mathématiques :
le nombre 1 - inutile de le présenter
le nombre pi -c'est pas sorcier non plus, c'est le rapport (constant) entre la circonférence d'un cercle et son rayon
le nombre i
là, c'est plus subtil ! Le nombre i est une construction des mathématiciens qui leur permet de résoudre l'équation i = racine carré de -1
on pose i.i = -1 et le tour est joué !
et on dit que i est un nombre "imaginaire" ! on invente alors l'ensemble des nombres imaginaires, puis les nombres complexes (un nombre complexe est la somme d'un nombre imaginaire plus un nombre réel) c=a+ib -le petit i est la pour rappeler que la partie a droite du + est un nombre imaginaire )
e est "la base des logarithmes néperiens" ou logarithmes "naturels C'est la "primitive" de la fonction 1/x -la valeur de la surface quand X varie de 0 a 1 est égale a ce fameux "e"
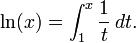
d'ou
ln (1) = e
le premier résultat que euler parvient a établir c'est

d'ou il va parvenir a établir la seconde relation
si vous voulez savoir comment on établi la premiere relation, on en déduit la seconde (ou n'importe quoi d'autre) suffit de le demander a sterd (pour une explication rigoureuse) ou a moi (pour une explication moins rigoureuse)