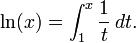Ce forum est animé et modéré par des militants et des sympathisants de Lutte Ouvrière.
Les opinions qui y sont exprimées le sont à titre personnel.
Elles n'engagent que leurs auteurs, et en aucune manière cette organisation.
Visitez le site officiel de Lutte Ouvrière • Consultez la charte du forum
Les opinions qui y sont exprimées le sont à titre personnel.
Elles n'engagent que leurs auteurs, et en aucune manière cette organisation.
Visitez le site officiel de Lutte Ouvrière • Consultez la charte du forum
la plus belle équation des maths !
23 message(s)
• Page 2 sur 3 • 1, 2, 3
par com_71 » 11 Oct 2006, 23:43
Si un complexe z s'écrit z=a+ib on voit qu'il faut pour former un complexe :
2 réels a et b
i (racine de -1)
définir la multiplication entre i et b
définir l'addition entre a et ib
Il faut bien voir que l'on est pas du tout dans la même catégorie de nombres qu'avec les réels. Par exemple il est impossible de dire qu'un complexe est plus grand qu'un autre...
L’intérêt ne pense pas, il calcule. Les motifs sont ses chiffres. K. Marx, « Débats sur la loi relative au vol de bois » 1842.
-
com_71 - Message(s) : 6415
- Inscription : 12 Oct 2002, 00:14
par Matrok » 12 Oct 2006, 00:06
Attention quand même, il y a plein de petites fautes dans tes explications LouisCR...
Non. C'est un nombre défini comme solution de l'équation "x^2 = -1". Ca peut paraître du chipotage, mais la fonction "racine carrée" est définie sur R+ et a solutions dans R+, ce qui veut dire que l'expression "racine carrée de -1" est abusive. Bon c'est pas très grave, cette bourde là :engels: l'a faite avant toi dans l'Anti Dhuring.
Attention : le logarithme népérien est non pas "la" primitive de la fonction inverse (la fonction qui a t associe 1/t) mais "une" primitive, en fait une primitive bien particulière : celle qui s'annule en 1. Ce qui correspond à la formule que tu as écrite. D'une manière plus imagée : c'est l'aire sous la courbe qui représente la fonction inverse, entre t=1 et t=x.
Argh ! non, c'est faux. De la formule précédente ce que tu peux tirer immédiatement c'est "ln(1) = 0" (autrement dit l'aire sous la courbe de 1/x entre t=1 et t=1 est nulle, on s'en doutait un peu). Ce qui ne nous dit toujours pas ce qu'est e. En fait e est défini comme solution de l'équation "ln(x) = 1" (autrement dit : e est le nombre tel que ln(e) = 1, on tel que l'aire sous la courbe de la fonction inverse entre 1 et e soit égale à 1).
Hum ! c'est court-circuiter une partie de l'histoire de la fonction exponentielle (pour ceux qui suivent difficilement : c'est la fonction qui a x associe e^x), que de laisser penser qu'à partir de la définition de e que tu as donnée on peut parvenir à cette relation... parce que jusqu'ici on n'a défini l'exponentielle que sur les réels !
En fait si mes souvenirs sont bons, il faut redéfinir l'exponentielle comme la limite quand n tend vers plus l'infini de :
1 + x + (x^2)/2 + (x^3)/6 + ... + (x^n)/n!
Il faut bien sûr entre temps montrer dans quel domaine cette fonction est définie, et montrer que sur les réels elle coincide avec la fonction exponentielle déja définie. Puis utiliser la nouvelle définition pour "prolonger" cette fonction aux complexes. Et enfin démontrer qu'on obtient la même chose qu'avec l'expression "cos(x) + i*sin(x)".
-------------------------------------------------------------
Pour com71 : attention avec l'écriture "log" pour le logarithme népérien. Aujourd'hui on réserve plutôt ça pour le logarithme décimal et on utilise ln pour le népérien.
(LouisChristianRené @ mercredi 11 octobre 2006 à 22:16 a écrit :le nombre i
là, c'est plus subtil ! Le nombre i est une construction des mathématiciens qui leur permet de résoudre l'équation i = racine carré de -1
Non. C'est un nombre défini comme solution de l'équation "x^2 = -1". Ca peut paraître du chipotage, mais la fonction "racine carrée" est définie sur R+ et a solutions dans R+, ce qui veut dire que l'expression "racine carrée de -1" est abusive. Bon c'est pas très grave, cette bourde là :engels: l'a faite avant toi dans l'Anti Dhuring.
a écrit :e est "la base des logarithmes néperiens" ou logarithmes "naturels" C'est la "primitive" de la fonction 1/x -la valeur de la surface quand X varie de 0 a 1 est égale a ce fameux "e"
Attention : le logarithme népérien est non pas "la" primitive de la fonction inverse (la fonction qui a t associe 1/t) mais "une" primitive, en fait une primitive bien particulière : celle qui s'annule en 1. Ce qui correspond à la formule que tu as écrite. D'une manière plus imagée : c'est l'aire sous la courbe qui représente la fonction inverse, entre t=1 et t=x.
a écrit :d'ou
ln (1) = e
Argh ! non, c'est faux. De la formule précédente ce que tu peux tirer immédiatement c'est "ln(1) = 0" (autrement dit l'aire sous la courbe de 1/x entre t=1 et t=1 est nulle, on s'en doutait un peu). Ce qui ne nous dit toujours pas ce qu'est e. En fait e est défini comme solution de l'équation "ln(x) = 1" (autrement dit : e est le nombre tel que ln(e) = 1, on tel que l'aire sous la courbe de la fonction inverse entre 1 et e soit égale à 1).
a écrit :le premier résultat que euler parvient a établir c'est
d'ou il va parvenir a établir la seconde relation
Hum ! c'est court-circuiter une partie de l'histoire de la fonction exponentielle (pour ceux qui suivent difficilement : c'est la fonction qui a x associe e^x), que de laisser penser qu'à partir de la définition de e que tu as donnée on peut parvenir à cette relation... parce que jusqu'ici on n'a défini l'exponentielle que sur les réels !
En fait si mes souvenirs sont bons, il faut redéfinir l'exponentielle comme la limite quand n tend vers plus l'infini de :
1 + x + (x^2)/2 + (x^3)/6 + ... + (x^n)/n!
Il faut bien sûr entre temps montrer dans quel domaine cette fonction est définie, et montrer que sur les réels elle coincide avec la fonction exponentielle déja définie. Puis utiliser la nouvelle définition pour "prolonger" cette fonction aux complexes. Et enfin démontrer qu'on obtient la même chose qu'avec l'expression "cos(x) + i*sin(x)".
-------------------------------------------------------------
Pour com71 : attention avec l'écriture "log" pour le logarithme népérien. Aujourd'hui on réserve plutôt ça pour le logarithme décimal et on utilise ln pour le népérien.
- Matrok
- Message(s) : 177
- Inscription : 12 Mars 2003, 21:43
par com_71 » 12 Oct 2006, 00:13
(Matrok @ jeudi 12 octobre 2006 à 01:06 a écrit :
Pour com71 : attention avec l'écriture "log" pour le logarithme népérien. Aujourd'hui on réserve plutôt ça pour le logarithme décimal et on utilise ln pour le népérien.
Bon, je me fais traiter d'homme d'hier...
:cry: :cry:L’intérêt ne pense pas, il calcule. Les motifs sont ses chiffres. K. Marx, « Débats sur la loi relative au vol de bois » 1842.
com_71- Message(s) : 6415
- Inscription : 12 Oct 2002, 00:14
par Gaby » 12 Oct 2006, 00:21
(com_71 @ jeudi 12 octobre 2006 à 01:13 a écrit :(Matrok @ jeudi 12 octobre 2006 à 01:06 a écrit :
Pour com71 : attention avec l'écriture "log" pour le logarithme népérien. Aujourd'hui on réserve plutôt ça pour le logarithme décimal et on utilise ln pour le népérien.
Bon, je me fais traiter d'homme d'hier...
:cry: :cry:
Vois le bon côté des choses, tu t'en souviens encore malgré tout ce temps, et moi qui ai planché dessus y'a pas 3 ans, je ne capte plus rien de rien... :ermm:
- Gaby
- Message(s) : 401
- Inscription : 27 Fév 2004, 10:53
par Sterd » 12 Oct 2006, 06:48
(Matrok @ jeudi 12 octobre 2006 à 00:16 a écrit : Relis bien l'expression :
e^(i*pi) + 1 = 0
Moi je vois 5 nombres, et ils sont tous "remarquables" à leur manière...
Et moi je ne sais même pas compter sur mes doigts, je les avait tous, mais je comptais 4. :emb:
- Sterd
- Message(s) : 0
- Inscription : 27 Nov 2005, 20:51
par shadoko » 13 Oct 2006, 13:48
a écrit :
Hum ! c'est court-circuiter une partie de l'histoire de la fonction exponentielle (pour ceux qui suivent difficilement : c'est la fonction qui a x associe e^x), que de laisser penser qu'à partir de la définition de e que tu as donnée on peut parvenir à cette relation... parce que jusqu'ici on n'a défini l'exponentielle que sur les réels !
En fait si mes souvenirs sont bons, il faut redéfinir l'exponentielle comme la limite quand n tend vers plus l'infini de :
1 + x + (x^2)/2 + (x^3)/6 + ... + (x^n)/n!
Il faut bien sûr entre temps montrer dans quel domaine cette fonction est définie, et montrer que sur les réels elle coincide avec la fonction exponentielle déja définie.
Disons que c'est la manière moderne et rigoureuse de définir l'exponentielle. Mais es-tu sûr que c'est comme cela qu'on a procédé historiquement? Je sais qu'Euler a effectivement donné la décomposition en série de e, mais je ne suis pas sûr du reste.
a écrit :
Puis utiliser la nouvelle définition pour "prolonger" cette fonction aux complexes. Et enfin démontrer qu'on obtient la même chose qu'avec l'expression "cos(x) + i*sin(x)".
En fait, là, c'est plutôt le contraire. Si on veut vraiment rester dans les définitions rigoureuses, on définit en général le cosinus et le sinus comme les parties réelle et imaginaire de l'exponentielle. Il n'y a donc rien à montrer dans cette formule, c'est une définition du terme de droite. En fait, la seule chose non triviale (mais pas très compliquée) à montrer dans cette histoire est que exp(x+y)=exp(x)exp(y) à partir de la définition en série.
- shadoko
- Message(s) : 2
- Inscription : 17 Juin 2004, 19:35
par Sterd » 14 Oct 2006, 06:47
(Louis @ vendredi 13 octobre 2006 à 21:48 a écrit : arggggg ! je m'apperçois a la relecture qu'on a oublié le principal : ces relations (eix=-1 et eix=cos x + i sin x) ne sont vrai que si on exprime les angles en pi radian (et pas en degré)
Je ne crois pas avoir jamais vu de fonctions trigonométriques travailler sur autre chose que des radians :33:
- Sterd
- Message(s) : 0
- Inscription : 27 Nov 2005, 20:51
23 message(s)
• Page 2 sur 3 • 1, 2, 3
Qui est en ligne ?
Utilisateur(s) parcourant ce forum : Aucun utilisateur inscrit et 1 invité